Exploring math with GeoGebra
GeoGebra is a fun, open source program for illustrating formulas and is a must for anyone interested in mathematics. One of the great things about GeoGebra is that it allows users to go beyond just geometry.
The project originated in Austria, sponsored by the Ministry of Culture. Currently, 49 developers from all over the world are working on GeoGebra along with the original author and current project leader, Markus Hohenwachter. Additionally, a huge team of translators are localizing the program into other languages.
GeoGebra can be found in most distribution repositories, including Ubuntu, and, therefore, can be installed with a button click; however, the version that comes with Ubuntu is the slightly older, stable version. The latest version is available at the GeoGebra website [1] and can be obtained by clicking the Download button.
You then have the choice between a webstart version for local installation and an applet. In the former case, the software ends up on your computer; in the latter case, it doesn't. The names are bit confusing because it would seem to be the other way around. The applet version presumes that you have a Java plugin, such as Iced Tea, installed. The advantage of the applet is primarily that it provides you the most current version, which at press time is GeoGebra 4.2. GeoGebra is additionally available in the form of archives for installing on Linux, Mac OS X, Windows and OLPC XO.
Geometry
Since its first version, GeoGebra has implemented a technique known as "dynamic geometry" that lets you explore geometric sets playfully using your mouse. You select icons from the toolbar and move points with your mouse in a coordinates display so that you can draw lines, circles, and polygons. These designs retain their properties even when moving their construction points (Figure 1).
 Figure 1: Moving points A, B, or C retains the basic structure: Perpendicular bisectors of a triangle intersect at the center of the circumference.
Figure 1: Moving points A, B, or C retains the basic structure: Perpendicular bisectors of a triangle intersect at the center of the circumference.
In this way, you easily learn the basic laws of plane geometry along with the vital mathematical concept that the geometrical construct stays the same even when its components are shifted. The idea of universality, of such great importance in mathematics, easily becomes apparent.
Tools
The GeoGebra toolbar includes a standard set of 12 groups of tools for working with objects. These include tools for moving, pointing, lines, special lines, polygons, circles and arcs, conic sections, measurement, transformation, and special and action objects. Other general and custom tools are included, along with spreadsheet views and the Computer Algebra System (CAS) – or functions for solving algebraic equations. Every tool group in GeoGebra contains numerous individual tools (Figure 2).
 Figure 2: The buttons under the menubar provide access to groups of tools. Click the down arrow in each group to see the individual selections.
Figure 2: The buttons under the menubar provide access to groups of tools. Click the down arrow in each group to see the individual selections.
Views
GeoGebra versions 4.0 and later highlight the use of "views," which are sub-windows of the program window. You can open as many views as you need – limited only by your computer's memory and CPU. Two of the views are especially important: algebra view and graphics view (Figure 3).
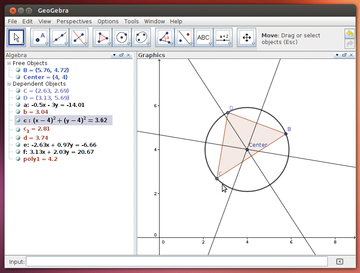 Figure 3: Selecting an object in the Graphics view shows the corresponding math values in the Algebra view.
Figure 3: Selecting an object in the Graphics view shows the corresponding math values in the Algebra view.
The current GeoGebra versions also provide Spreadsheet and CAS views, and the Beta 5.0 [2] version adds a 3D view. The beta version shows where GeoGebra is going: It wants to become the universal mathematics program.
This description includes the new features of Beta 5.0; however, the project warns against pulling that version into applications just yet because of its many serious bugs. The data structures can also still change.
Special attention should be given to the entry line at the bottom of each view. There, you can directly define mathematical objects, for example by specifying point A with its coordinates A=(1, 2) , where x=1 , y=2 .
To the right of the entry field are arrows that you can use to reenter previously defined values. Once you click on the arrow of the input field, to the right of the graphics view an entry field opens for further mathematical functions (Figure 4).
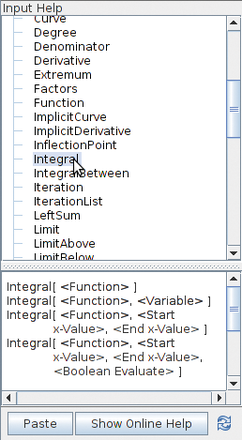 Figure 4: If you choose a tool (in this case, Integral), the software shows the syntax of the command, which you can move to the entry field by clicking a button.
Figure 4: If you choose a tool (in this case, Integral), the software shows the syntax of the command, which you can move to the entry field by clicking a button.
Didactic Nightmare?
Version 4.x has commands that can make GeoGebra a universal system for schools. By entering functions, extrema, and inflection points, you can create an instructional example of a classic curve with a simple mouse click (Figure 5).
The example in Figure 5 illustrates, however, that math software doesn't replace knowledge. Pointlessly pressing buttons will not always lead to meaningful results, but software can help explain basic concepts. Neither GeoGebra nor any other programs, however, can explain why the curve's (0, 0 ) coordinates are its inflection point. Only those schooled in the concept can answer that question.
Sticking by this principle as a teacher doesn't mean changing your instruction methods when using GeoGebra as a tool. The software simply gives students indications of things to discover. Incidentally, a possibly simpler explanation for the curve might be gained by using the Function Inspector tool (Figure 6).
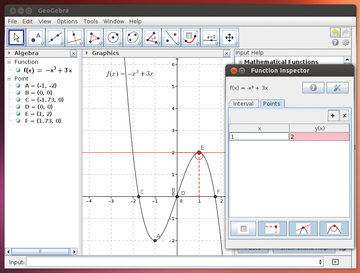 Figure 6: The Function Inspector calculates at a specified point the coordinates, tangent, and radius of the curve.
Figure 6: The Function Inspector calculates at a specified point the coordinates, tangent, and radius of the curve.
Meanwhile, the "GeoGebra for Tablets" project is ushering in a further developmental phase: GeoGebra on mobile phones. Many teachers might be annoyed by increased surreptitious googling during class, but with applications such as GeoGebra, the smartphone becomes a natural pedagogic device. Students can use mobile phones during instruction and, in return, get a first-class tool that replaces the calculator.
Materials
Students are hardly thrilled when teachers continually introduce new applications for them to work with, but this is exactly what the Featured Materials [3] collection for GeoGebra provides. The idea is not only to provide a library of applications for teachers, but also to provide input to software authors from teachers and students alike. The collection contains highly educational material, mainly from physics, and GeoGebra also provides aids to visualization (Figure 7).
Of much greater importance than prefabricated applications, however, is the option to use GeoGebra as a tool for your own work. In particular, analyzing data sets and exporting them as image files during science instruction provides an excellent opportunity for students to participate actively. Exporting the data also allows porting a self-developed application as an HTML file to a website or a Moodle course.
Setting in Motion
The software lets you assign variables with assigned ranges to points. You can activate this feature by selecting a point in Graphics view with the Move tool. The corresponding controller then passes through the region in either one direction or reverses direction at the end. The construct changes accordingly in all associated properties.
Figure 8 shows the tabular results of a case study. A right mouse click creates a series of points in Graphics view from the values for the fields A2 through B8 . Next, in the entry field, you can enter the presumed function for an undetermined parameter. A very good regression will yield the function s(x)=a*x^2 for the value a=4.5 .
 Figure 8: The ability to input variable values for points allows regression and the location of features by repeated trials.
Figure 8: The ability to input variable values for points allows regression and the location of features by repeated trials.
New and Newer
Although CAS view was introduced in GeoGebra 5.0, version 4.2 already has CAS capability for finding zeroes or extrema. But much more exciting is the step into the third dimension. Previously, many CAS systems provided vector analysis, but the visualization was missing. GeoGebra is now the first open source program to venture into implementing this feature (Figure 9).
 Figure 9: The 3D view allows you to enter points on a 3D coordinate system; GeoGebra creates the corresponding constructs, making it possible to illustrate the results of vector calculations.
Figure 9: The 3D view allows you to enter points on a 3D coordinate system; GeoGebra creates the corresponding constructs, making it possible to illustrate the results of vector calculations.
The 3D view provides a separate set of tool groups, such as those for cutting surfaces, defining surfaces and spheres differently, and rotating coordinates.
Additionally, if you previously missed the opportunity for programming, GeoGebra 5.0 now provides a Python view so you can create your own programs and build them into constructs.
Conclusion
GeoGebra, previously a simple program for dynamic geometry, has steadily developed into a universal math application – at least, that's what version 5.0 implies. The GeoGebra for Tablets project also charts its future on mobile devices. GeoGebra's performance spectrum stretches from a simple visualization system to a tool for complex data analysis and mathematical relationships.
The speed at which GeoGebra is being developed is stunning, and the interaction with users sets an excellent example. A huge library of excellent applications, all under the GPL, are also available for immediate download.
Infos
- GeoGebra: https://www.geogebra.org/cms/
- GeoGebra 5.0 Beta: http://www.geogebra.org/forum/viewtopic.php?f=52&t=19846
- Featured materials: http://www.geogebratube.org/?lang=en


