Exploring math with GeoGebra

Views

GeoGebra versions 4.0 and later highlight the use of "views," which are sub-windows of the program window. You can open as many views as you need  – limited only by your computer's memory and CPU. Two of the views are especially important: algebra view and graphics view (Figure 3).

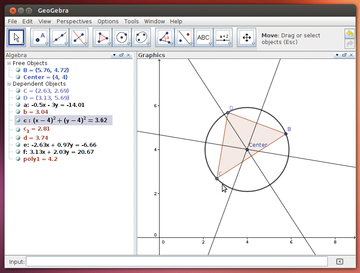Figure 3: Selecting an object in the Graphics view shows the corresponding math values in the Algebra view.

The current GeoGebra versions also provide Spreadsheet and CAS views, and the Beta 5.0 [2] version adds a 3D view. The beta version shows where GeoGebra is going: It wants to become the universal mathematics program.

This description includes the new features of Beta 5.0; however, the project warns against pulling that version into applications just yet because of its many serious bugs. The data structures can also still change.

Special attention should be given to the entry line at the bottom of each view. There, you can directly define mathematical objects, for example by specifying point A with its coordinates A=(1, 2) , where x=1 , y=2 .

To the right of the entry field are arrows that you can use to reenter previously defined values. Once you click on the arrow of the input field, to the right of the graphics view an entry field opens for further mathematical functions (Figure 4).

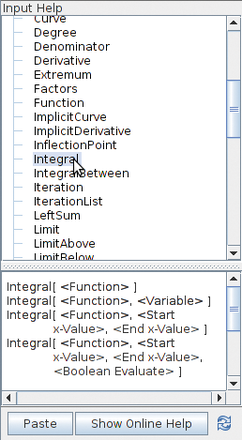Figure 4: If you choose a tool (in this case, Integral), the software shows the syntax of the command, which you can move to the entry field by clicking a button.

Didactic Nightmare?

Version 4.x has commands that can make GeoGebra a universal system for schools. By entering functions, extrema, and inflection points, you can create an instructional example of a classic curve with a simple mouse click (Figure 5).

Figure 5: With four entries, you can construct the curve with all its properties.

The example in Figure 5 illustrates, however, that math software doesn't replace knowledge. Pointlessly pressing buttons will not always lead to meaningful results, but software can help explain basic concepts. Neither GeoGebra nor any other programs, however, can explain why the curve's (0, 0 ) coordinates are its inflection point. Only those schooled in the concept can answer that question.

Sticking by this principle as a teacher doesn't mean changing your instruction methods when using GeoGebra as a tool. The software simply gives students indications of things to discover. Incidentally, a possibly simpler explanation for the curve might be gained by using the Function Inspector tool (Figure 6).

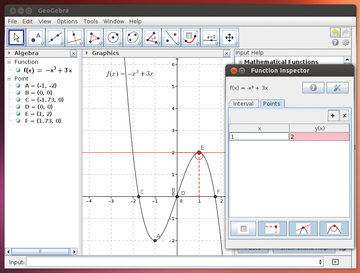Figure 6: The Function Inspector calculates at a specified point the coordinates, tangent, and radius of the curve.

Meanwhile, the "GeoGebra for Tablets" project is ushering in a further developmental phase: GeoGebra on mobile phones. Many teachers might be annoyed by increased surreptitious googling during class, but with applications such as GeoGebra, the smartphone becomes a natural pedagogic device. Students can use mobile phones during instruction and, in return, get a first-class tool that replaces the calculator.